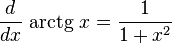ày+àn.... + Llam logx/x n... [*R, 0 –R [A] logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx + rot, + transl. + acel /t /c/t + [ logx/x n... [*R, 0 –R [A]* ocfp /c/t].
Derivadas de funções exponenciais e logarítmicas
 +
+
logx/x n... [*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .
Derivadas de
funções trigonométricas
funções trigonométricas
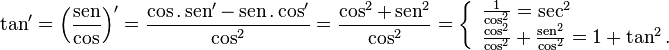
+
logx/x n... [*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .
 , ou, dito de outra maneira,
, ou, dito de outra maneira,  ; +
; +
logx/x n... [*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .
 , ou, dito de outra maneira,
, ou, dito de outra maneira, 
+
logx/x n...
[*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .
 , ou, dito de outra maneira,
, ou, dito de outra maneira, 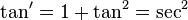
+
logx/x n...
[*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .

+
logx/x n...
[*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .
 , ou, dito de outra maneira,
, ou, dito de outra maneira, 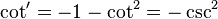
+
logx/x n...
[*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .

+
logx/x n...
[*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .

+
logx/x n...
[*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .
+
logx/x n...
[*R, 0 –R [A]
logx/x....+ â
[grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx .